AtCoder Beginner Contest 347 A-G 题解
A - Divisible
Quesiton
给你正整数
提取
Solution
判断
Code
#include <bits/stdc++.h>
using namespace std;
int main() {
vector<int> ans;
int n, k; cin >> n >> k;
for (int i = 1; i <= n;i++) {
int x; cin >> x;
if (x % k == 0) {
ans.push_back(x / k);
}
}
for (auto x : ans)
cout << x << " ";
return 0;
}
B - Substring
Question
给你一个由小写英文字母组成的字符串
子串是连续的子序列。例如,xxx是yxxxy的子串,但不是xxyxx的子串。
Solution
使用 substr() 函数取字串
然后用 set<string> 去重即可
Code
#include <bits/stdc++.h>
using namespace std;
int main() {
string s; cin >> s;
set<string> st;
for (int L = 1; L <= s.size(); L++)
for (int i = 0; i + L - 1 < s.size(); i++) {
string t = s.substr(i, L);
st.insert(t);
}
cout << st.size() << endl;
return 0;
}
C - Ideal Holidays
Soluiton
考虑把一个
即
我们需要找一个
如果
具体实现是,转化为判断
排序后,是否存在一个
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
int n; cin >> n;
ll A, B; cin >> A >> B;
vector<ll> D(n);
for (int i = 0; i < n; i++) {
cin >> D[i];
D[i] = (D[i] - 1) % (A + B);
}
sort(D.begin(), D.end());
for (int i = 1; i < n; i++)
if (D[i] - D[i - 1] >= B) {
cout << "Yes" << '\n';
return 0;
}
if (D.back() - D.front() < A) {
cout << "Yes" << '\n';
return 0;
}
cout << "No" << endl;
return 0;
}
D - Popcount and XOR
Solution
由于异或的性质,每一位分开来看,如果为
我们设
所以
然后模拟放
如果
在
使用 bitset 可以很好的模拟
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
int a, b;
ll C;
cin >> a >> b >> C;
bitset<60> bit_C(C), bit_A, bit_B;
if (a + b < bit_C.count() || (a + b - bit_C.count()) % 2 == 1) {cout << "-1" << '\n'; return 0;}
int cnt = (a + b - bit_C.count()) / 2;
a -= cnt; b -= cnt;
for (int i = 0; i < 60; i++) {
if (bit_C[i]) {
if (a) {bit_A[i] = 1; a--;}
else if (b) {bit_B[i] = 1; b--;}
}
}
if (a != 0 || b != 0) {cout << "-1" << '\n'; return 0;}
for (int i = 0; i < 60; i++)
if (bit_C[i] == 0)
if (cnt) {
bit_A[i] = 1; bit_B[i] = 1; cnt--;
}
if (cnt) {cout << "-1" << '\n'; return 0;}
cout << bit_A.to_ullong() << ' ' << bit_B.to_ullong() << '\n';
return 0;
}
E - Set Add Query
Solution
提前用 set<int> 模拟出第
对于每个数,答案就是,奇数次出现
直接用树状数组或前缀和就可以快速得到
如果最后一个是奇数次,那么就加上个点到最后所有的
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
freopen ("E.in","r",stdin);
int n, Q; cin >> n >> Q;
vector<int> q(Q + 1, 0);
for (int i = 1; i <= Q; i ++)
cin >> q[i];
set<int> st;
vector<ll> cnt(Q + 1, 0);
for (int i = 1; i <= Q; i++) {
int x = q[i];
if (st.count(x))
st.erase(x);
else
st.insert(x);
cnt[i] = st.size();
}
vector<vector<int> > pos(n + 1, vector<int>());
for (int i = 1; i <= Q; i++)
pos[q[i]].push_back(i);
vector<ll> c(Q + 1, 0);
auto add = [&](int x, int v) {
for (; x <= Q; x += x & -x)
c[x] += v;
};
auto query = [&](int x) {
ll res = 0;
for (; x; x -= x & -x)
res += c[x];
return res;
};
for (int i = 1; i <= Q; i++)
add(i, cnt[i]);
for (int i = 1; i <= n; i++) {
ll ans = 0;
if (pos[i].size() & 1)
pos[i].push_back(Q + 1);
for (int j = 0; j < pos[i].size(); j += 2) {
ans += query(pos[i][j + 1] - 1) - query(pos[i][j] - 1);
}
cout << ans << ' ';
}
return 0;
}
F - Non-overlapping Squares
Solution
先考虑两个
显然,存在一条线,把
所以推广到三个
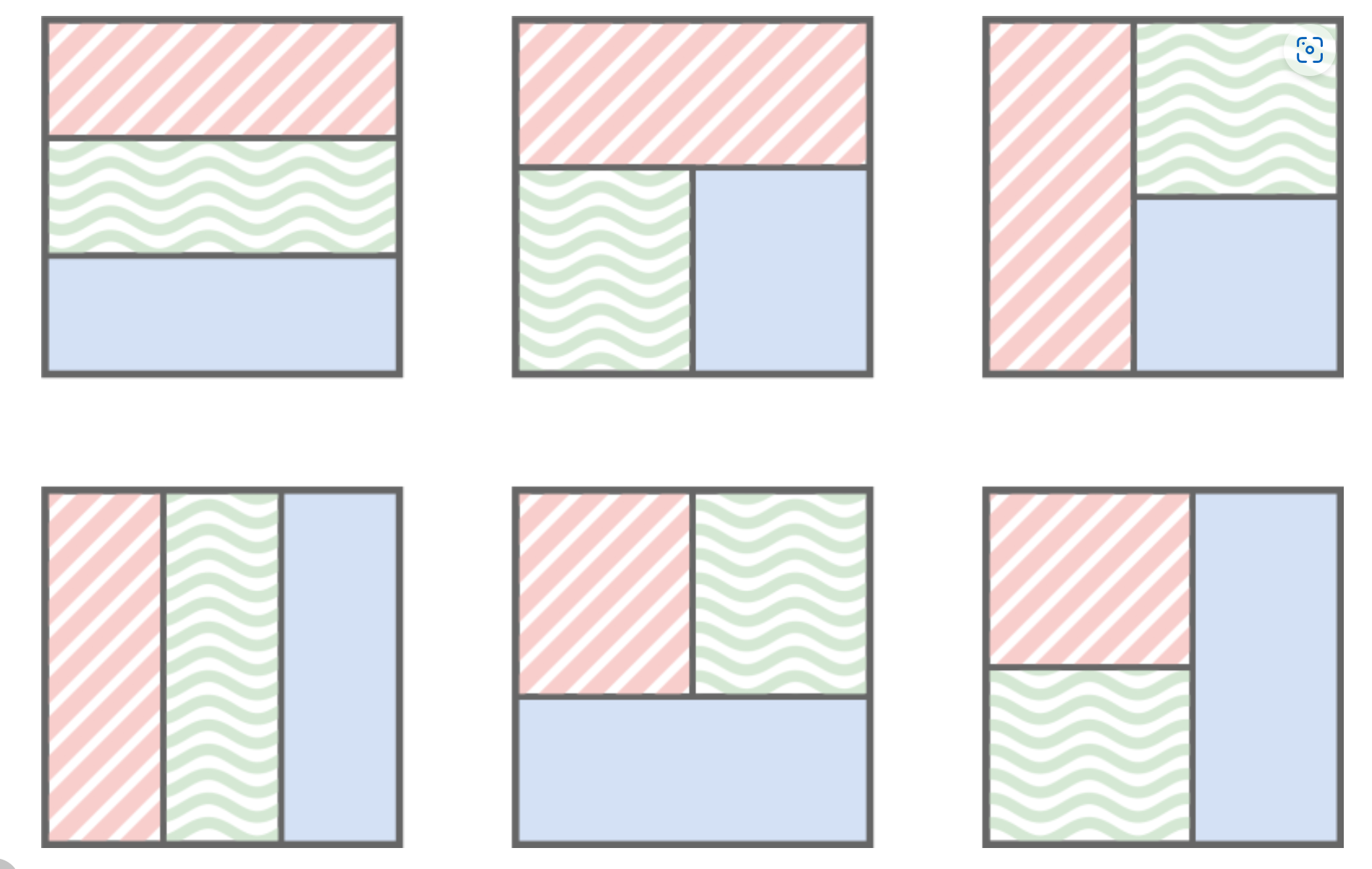
每个
我们先求出每个点为右下角作的点的
然后对于每个单独的矩形块,只需要找矩形内的最大值即可
可以使用线段树套线段树解决,时间复杂度为
我在具体实现时只写了三个,然后通过旋图去求另外三个
Code
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf = 1e17;
const int maxn = 1e3 + 1;
ll maxv[maxn << 2][maxn << 2];
struct Segment_Tree {
int n;
void build_y (int u, int rt, int l, int r) {
maxv[rt][u] = -inf;
if (l == r) return;
int mid = (l + r) >> 1;
build_y(u << 1, rt, l, mid);
build_y(u << 1 | 1, rt, mid + 1, r);
}
void build_x (int u, int l, int r) {
build_y (1, u, 1, n);
if (l == r) return;
int mid = (l + r) >> 1;
build_x(u << 1, l, mid);
build_x(u << 1 | 1, mid + 1, r);
}
void init(int _n) {
n = _n;
build_x(1, 1, n);
}
void update_y(int u, int rt, int l, int r, int y, ll val) {
if (l == r) {
maxv[rt][u] = max(maxv[rt][u], val);
return;
}
int mid = (l + r) >> 1;
if (y <= mid) update_y(u << 1, rt, l, mid, y, val);
else update_y(u << 1 | 1, rt, mid + 1, r, y, val);
maxv[rt][u] = max(maxv[rt][u << 1], maxv[rt][u << 1 | 1]);
}
void update_x(int u, int l, int r, int x, int y, ll val) {
update_y(1, u, 1, n, y, val);
if (l == r) return;
int mid = (l + r) >> 1;
if (x <= mid) update_x(u << 1, l, mid, x, y, val);
else update_x(u << 1 | 1, mid + 1, r, x, y, val);
}
ll query_y (int u, int rt, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr)
return maxv[rt][u];
int mid = (l + r) >> 1;
ll res = -inf;
if (ql <= mid)
res = max(res, query_y(u << 1, rt, l, mid, ql, qr));
if (qr > mid)
res = max(res, query_y(u << 1 | 1, rt, mid + 1, r, ql, qr));
return res;
}
ll query_x (int u, int l, int r, int qlx, int qrx, int qly, int qry) {
if (qlx <= l && r <= qrx)
return query_y (1, u, 1, n, qly, qry);
int mid = (l + r) >> 1;
ll res = -inf;
if (qlx <= mid)
res = max(res, query_x(u << 1, l, mid, qlx, qrx, qly, qry));
if (qrx > mid)
res = max(res, query_x(u << 1 | 1, mid + 1, r, qlx, qrx, qly, qry));
return res;
}
}st;
ll sum[maxn][maxn], a[maxn][maxn];
ll solve (int n, int m, vector<vector<ll> >& mp) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + mp[i][j]; // 2维前缀和
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (i < m || j < m) { a[i][j] = -inf; continue; }
a[i][j] = sum[i][j] - sum[i - m][j] - sum[i][j - m] + sum[i - m][j - m]; // 2维区间和
}
st.init(n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
st.update_x(1, 1, n, i, j, a[i][j]);
ll ans = -inf, now_1, now_2, now_3;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (i >= m && j - i >= m && n - j >= m) {
now_1 = st.query_x (1, 1, n, 1, n, 1, i);
now_2 = st.query_x (1, 1, n, 1, n, i + m, j);
now_3 = st.query_x (1, 1, n, 1, n, j + m, n);
ans = max(ans, now_1 + now_2 + now_3);
}
if (i >= m && j >= m && n - j >= m && n - i >= m) {
now_1 = st.query_x (1, 1, n, 1, i, 1, n);
now_2 = st.query_x (1, 1, n, i + m, n, 1, j);
now_3 = st.query_x (1, 1, n, i + m, n, j + m, n);
ans = max(ans, now_1 + now_2 + now_3);
}
if (i >= m && n - i >= m && j >= m && n - j >= m) {
now_1 = st.query_x (1, 1, n, i + m, n, 1, n);
now_2 = st.query_x (1, 1, n, 1, i, 1, j);
now_3 = st.query_x (1, 1, n, 1, i, j + m, n);
ans = max(ans, now_1 + now_2 + now_3);
}
}
return ans;
}
inline ll read_ll() {
ll x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
return x * f;
}
inline int read_int() {
int x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
return x * f;
}
int main() {
freopen ("F.in", "r", stdin);
freopen ("F.out", "w", stdout);
int n, m; n = read_int(); m = read_int();
vector<vector<ll> > mp(n + 1, vector<ll>(n + 1, 0)), sum(n + 1, vector<ll>(n + 1, 0));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
mp[i][j] = read_ll();
ll ans = solve(n, m, mp);
for (int k = 0; k < 1; k++) {
// rotate 90 degree
vector<vector<ll> > tmp(n + 1, vector<ll>(n + 1, 0));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
tmp[i][j] = mp[j][n - i + 1];
mp = tmp;
ans = max(ans, solve(n, m, mp));
}
cout << ans << endl;
return 0;
}
G - Grid Coloring 2
Solution
非常有意思一个题
我们利用拆点的思想,把问题转化成一个网络流模型
把一个点拆成 4 个点
然后建立一个超级原点
考虑这样建边:
(1) 对于每个点
建边

这保证了,
(2) 对于一个点
如果
如果

这保证了,
(3) 对于与
建边
建边
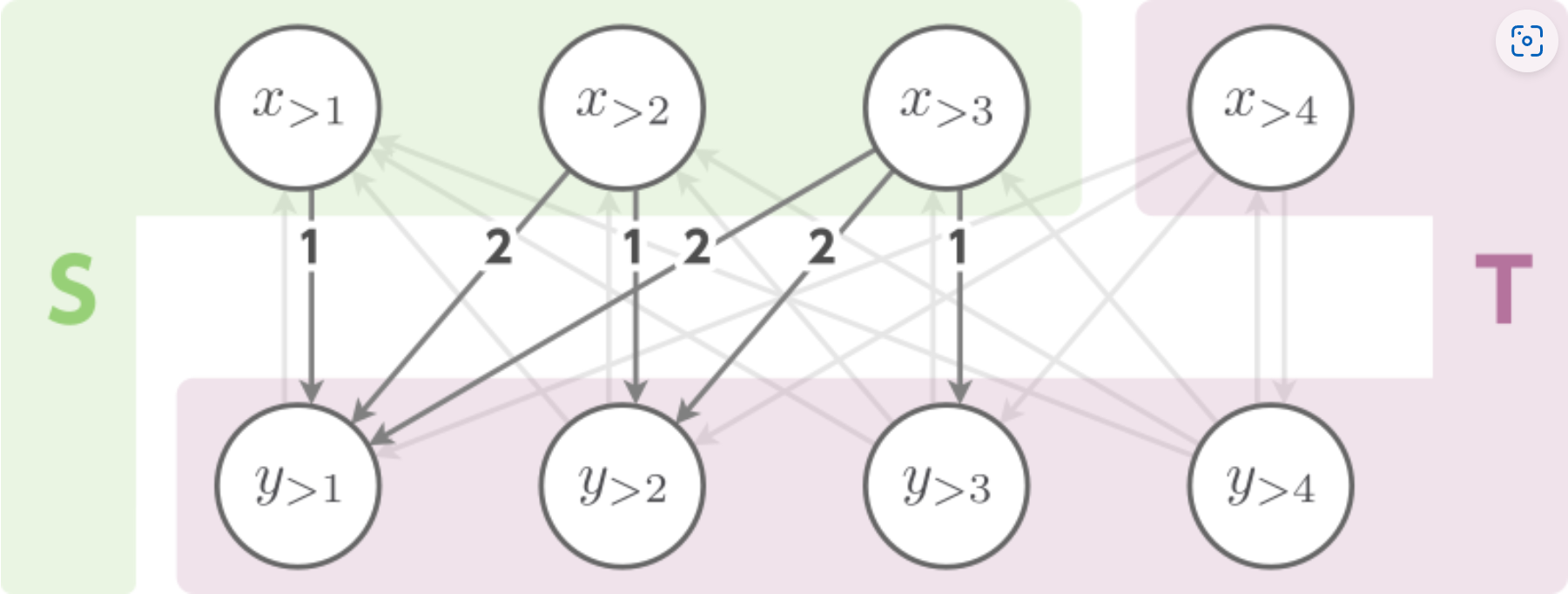
这里用到了一个很妙的性质,
此时
则所需要的代价就是
如果
则
Code
#include <bits/stdc++.h>
#include <atcoder/maxflow>
using namespace std;
const int inf = 0x3f3f3f3f;
int main() {
int n; cin >> n;
atcoder::mf_graph<int> g(1 + 4 * n * n + 1);
const int S = 0, T = 1 + 4 * n * n;
const auto id = [&] (int x, int y, int v) {
return (x * n + y) * 4 + v;
};
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
for (int v = 1; v + 1 <= 4; v++)
g.add_edge(id(i, j, v + 1), id(i, j, v), inf);
for (int i = 0; i < n; i++)
for (int j = 0; j + 1 < n; j++)
for (int v = 1; v <= 4; v++) {
g.add_edge(id(i, j, v), id(i, j + 1, v), 1);
g.add_edge(id(i, j + 1, v), id(i, j, v), 1);
for (int u = 1; u < v; u++) {
g.add_edge(id(i, j, v), id(i, j + 1, u), 2);
g.add_edge(id(i, j + 1, v), id(i, j, u), 2);
}
}
for (int i = 0; i + 1 < n; i++)
for (int j = 0; j < n; j++)
for (int v = 1; v <= 4; v++) {
g.add_edge(id(i, j, v), id(i + 1, j, v), 1);
g.add_edge(id(i + 1, j, v), id(i, j, v), 1);
for (int u = 1; u < v; u++) {
g.add_edge(id(i, j, v), id(i + 1, j, u), 2);
g.add_edge(id(i + 1, j, v), id(i, j, u), 2);
}
}
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
int x; cin >> x;
if (x == 0) continue;
if (x < 5)
g.add_edge(id(i, j, x), T, inf);
if (x > 1)
g.add_edge(S, id(i, j, x - 1), inf);
}
g.flow(S, T);
const auto &cut = g.min_cut(S);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
int x = 1;
for (int v = 1; v <= 4; v++)
x += cut[id(i, j, v)];
cout << x << ' ';
}
cout << '\n';
}
return 0;
}